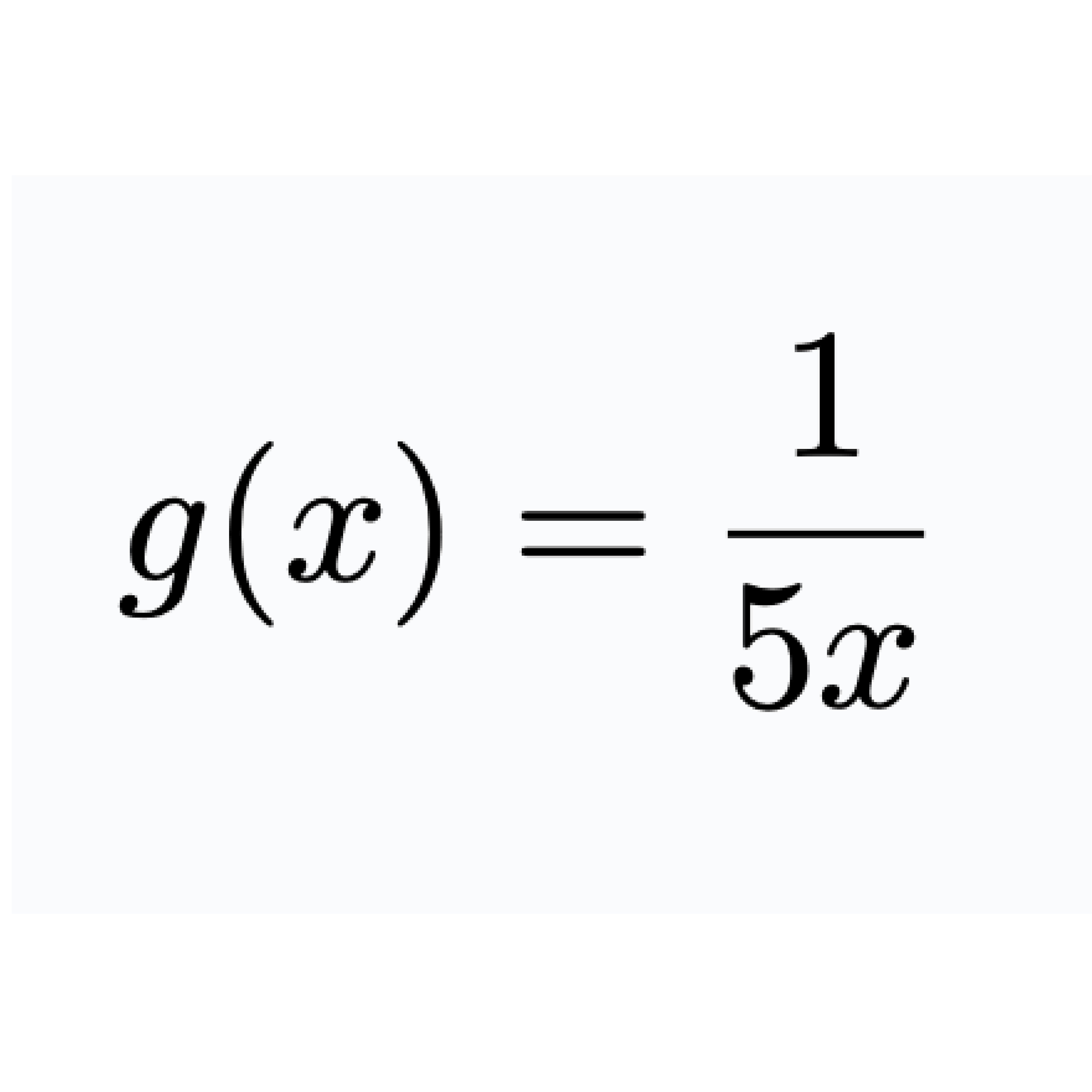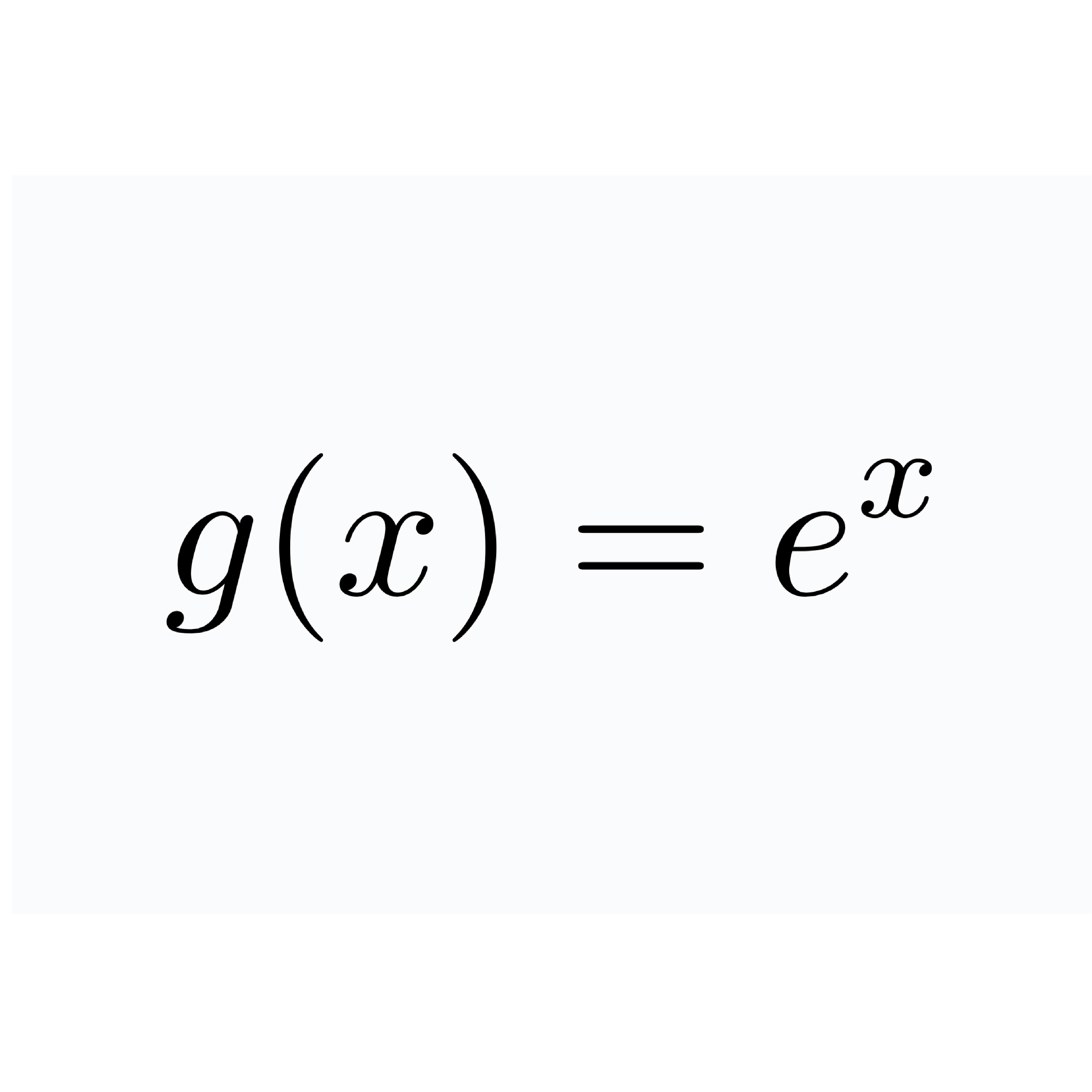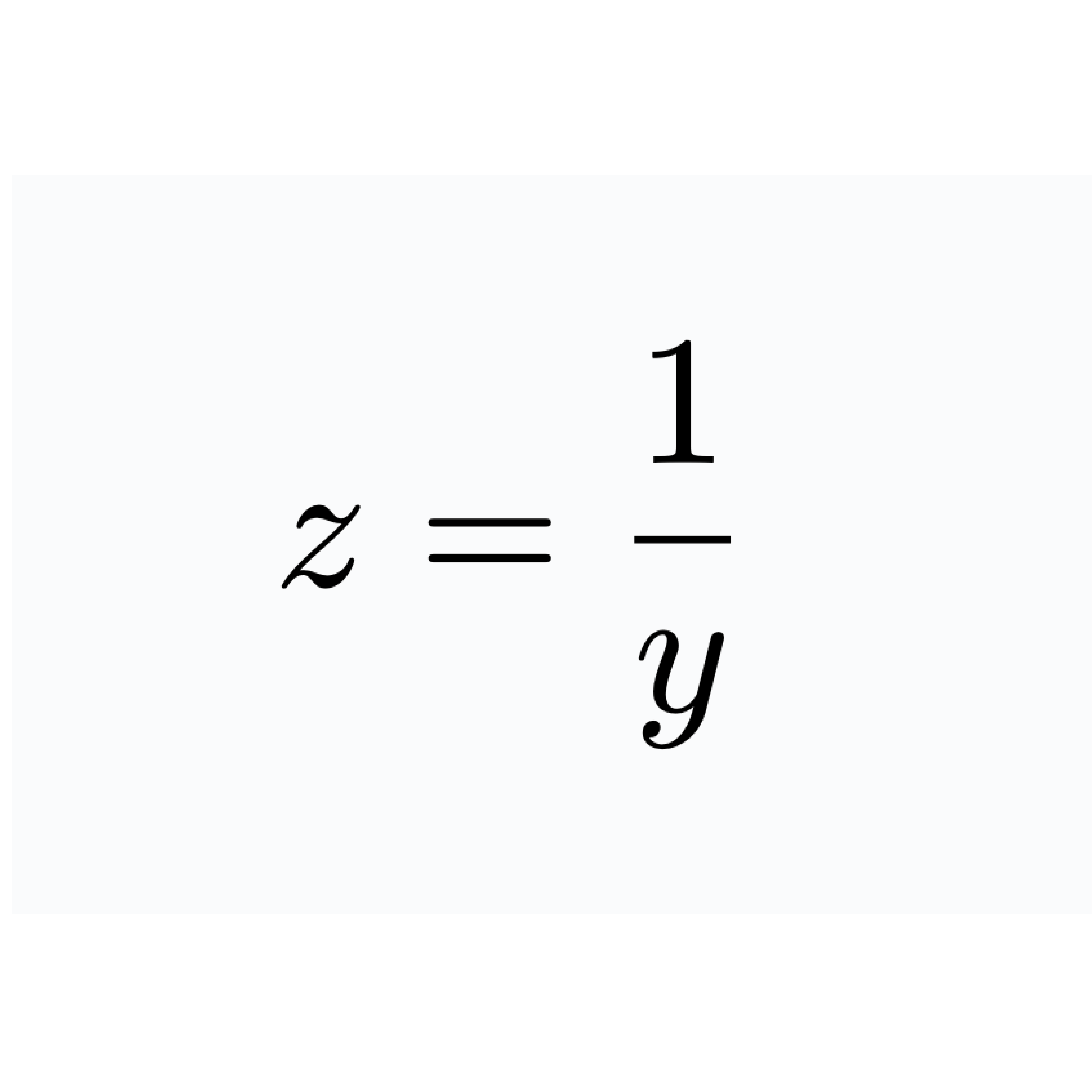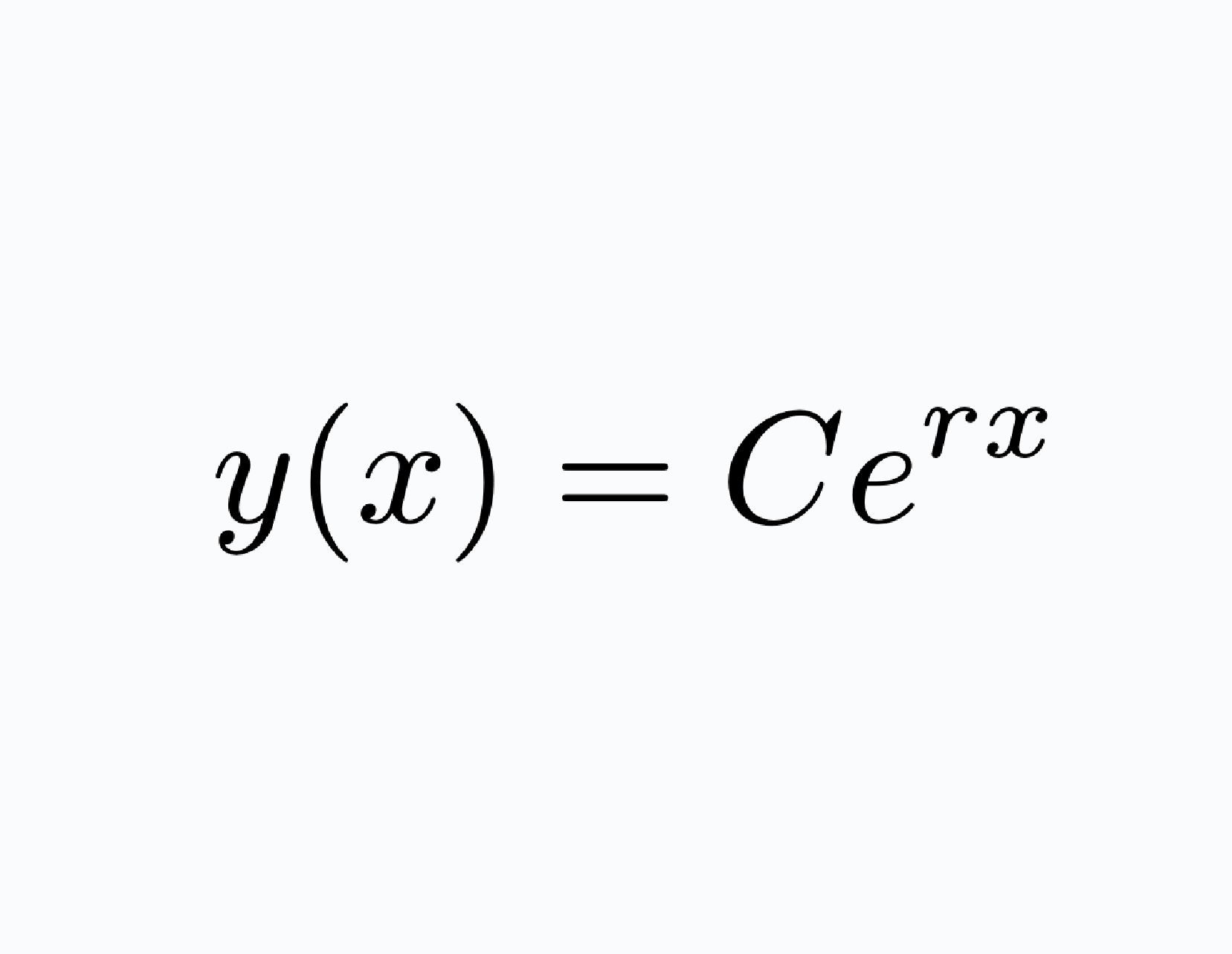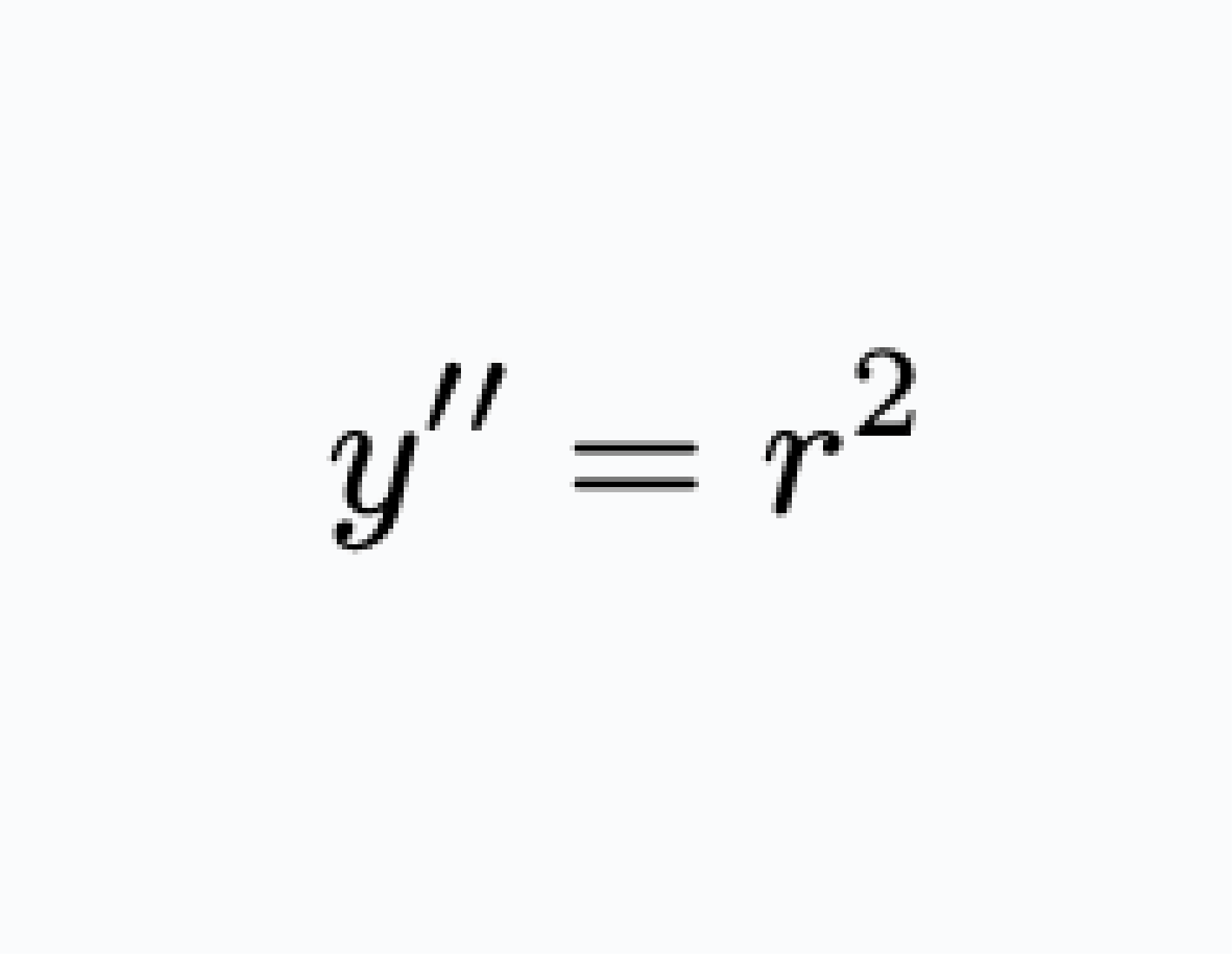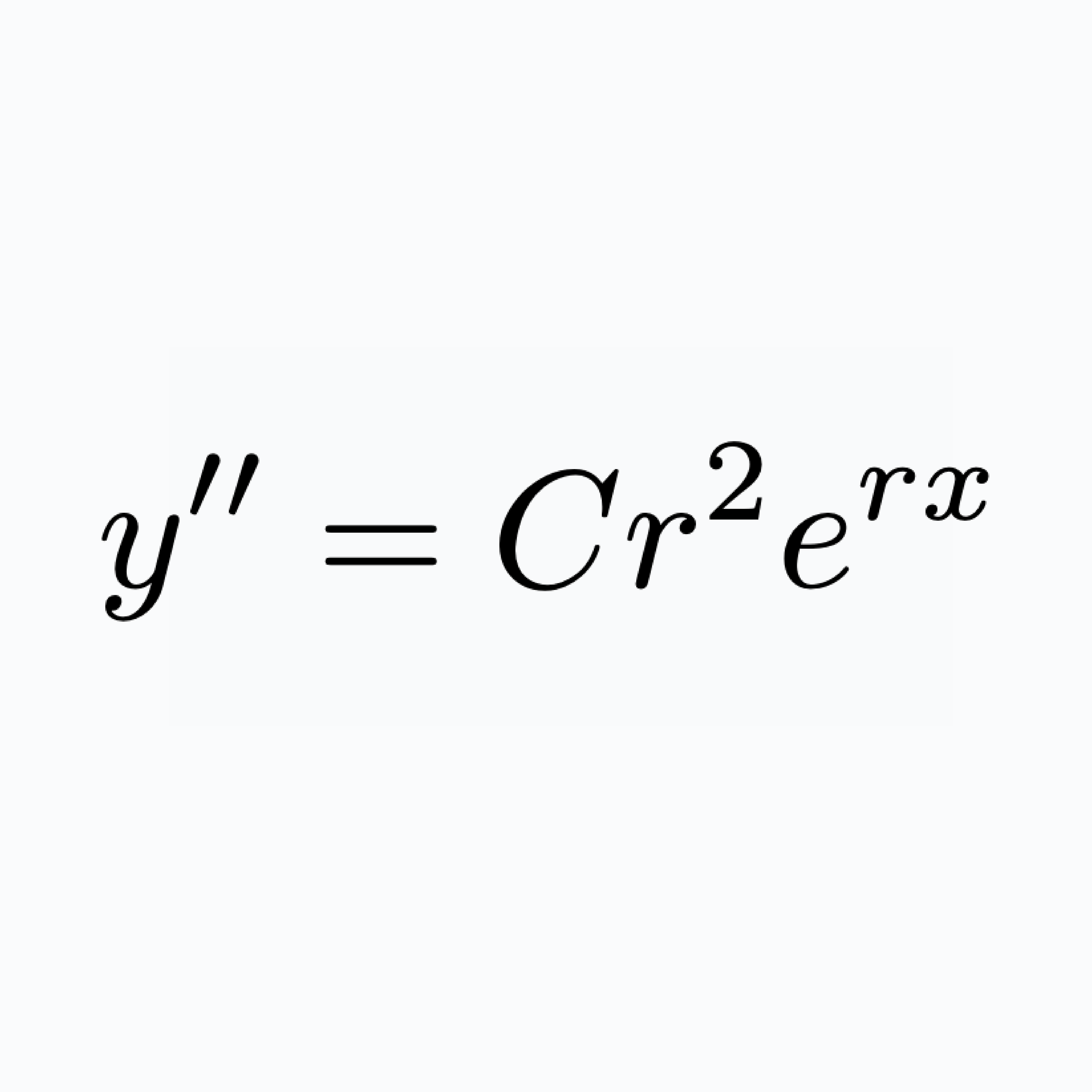Równania różniczkowe

Kurs z równań różniczkowych oferuje kompleksowy pakiet edukacyjny zawarty w dokumentach PDF, pokrywających szeroki zakres tematów związanych z tą dziedziną matematyki. Materiały te dostarczają kluczowych informacji na temat równań o zmiennych rozdzielonych, równań liniowych o stałych współczynnikach oraz równań bernouliego. By skorzystać z udostępnionych kodów niezbędne jest pobranie biblioteki dynpy dostępnej w przycisku poniżej. Wybrany kod należy następnie wkleić do projektu Jupyter Notebook.


Biblioteka dynpy

Pobierz PDF z rozwiązanym zadaniem

Wyświelt kod źródłowy

1. Równania o zmiennych rozdzielonych

Równanie z funkcjami trygonometrycznymi

Przykład pokazujący na funkcji trygonometrycznej metodologię rozwiązywania równań różniczkowych o zmiennych rozdzielonych.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff(x)*sin(x)-y*cos(x),0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #w celu wywołania współczynników zmiennych rozdzielonych (odpowiednio x,y)
                                    odesys._function_separation()

                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()

                                    #aby uzyskać rozwiązanie
                                    odesys._ode_solution()

                                    #aby wygenerować raport z rozwiązaniem
                                    odesys.report

Równanie z funkcją kwadratową

Przykład pokazujący na funkcji kwadratowej metodologię rozwiązywania równań różniczkowych o zmiennych rozdzielonych.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(2*x**2*y.diff(x)+y,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #w celu wywołania współczynników rozdzielonych zmiennych (odpowiednio x,y)
                                    odesys._function_separation()

                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiazaniem
                                    odesys.report

Równanie z funkcją liniową

Przykład pokazujący na funkcji liniowej metodologię rozwiązywania równań różniczkowych o zmiennych rozdzielonych.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*
                                    
                                    x=Symbol('x')
                                    y=Function('y')(x)
                                    
                                    #tu wprowadzić równanie:
                                    eq=Eq(5*x*y.diff(x)+y,0)
                                    
                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)
                                    
                                    #w celu wywołania współczynników rozdzielonych zmiennych (odpowiednio x,y)
                                    odesys._function_separation()
                                    
                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()
                                    
                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()
                                    
                                    #aby wygenerowac raport z rozwiazaniem
                                    odesys.report

2. Równiania liniowe

Równanie z funkcją liniową

Przykład pokazujący na funkcji liniowej metodologię rozwiązywania liniowych równań różniczkowych o stałych współczynnikach.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(-6+y.diff()-8*x+2*y,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

Równanie funkcją trygonometryczną

Przykład pokazujący na funkcji trygonometrycznej metodologię rozwiązywania liniowych równań różniczkowych o stałych współczynnikach.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff()+y*cos(x)-sin,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

Równanie z funkcją wykładniczą

Przykład pokazujący na funkcji wykładniczej metodologię rozwiązywania liniowych równań różniczkowych o stałych współczynnikach.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff(x)-exp(2*x)-y*exp(x),0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

3. Równania Bernoulliego

Równanie z funkcją kwadratową

Przykład pokazujący na funkcji kwadratowej metodologię rozwiązywania równań różniczkowych typu Bernoulliego.

PDF

 
                              

                                from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                from sympy import*

                                x=Symbol('x')
                                y=Function('y')(x)

                                #tu wprowadzić równanie:
                                eq=Eq(y+x*y.diff(x)+x*y**2,0)

                                # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                odesys=BernoulliODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                #w celu wywołania podstawień typowych dla rownan bernoulliego
                                odesys._bernoulli_substitution()

                                #w celu wywołania najwyższej potegi naszego rownania uzywamy metody:
                                odesys.get_nonlinear_power()

                                #aby uzyskac rozwiazanie
                                odesys._ode_solution()

                                #aby wygenerowac raport z rozwiazaniem
                                odesys.report

Równanie z funkcją trygonometryczną

Przykład pokazujący na funkcji trygonometrycznej metodologię rozwiązywania równań różniczkowych typu Bernoulliego.

PDF

 
                              

                                from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                from sympy import*
                                
                                x=Symbol('x')
                                y=Function('y')(x)
                                
                                #tu wprowadzić równanie:
                                eq=Eq(y+x*y.diff(x)+x*y**2,0)
                                
                                # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                odesys=BernoulliODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)
                                
                                #w celu wywołania podstawień typowych dla rownan bernoulliego
                                odesys._bernoulli_substitution()
                                
                                #w celu wywołania najwyższej potegi naszego rownania uzywamy metody:
                                odesys.get_nonlinear_power()
                                
                                #aby uzyskac rozwiazanie
                                odesys._ode_solution()
                                
                                #aby wygenerowac raport z rozwiazaniem
                                odesys.report