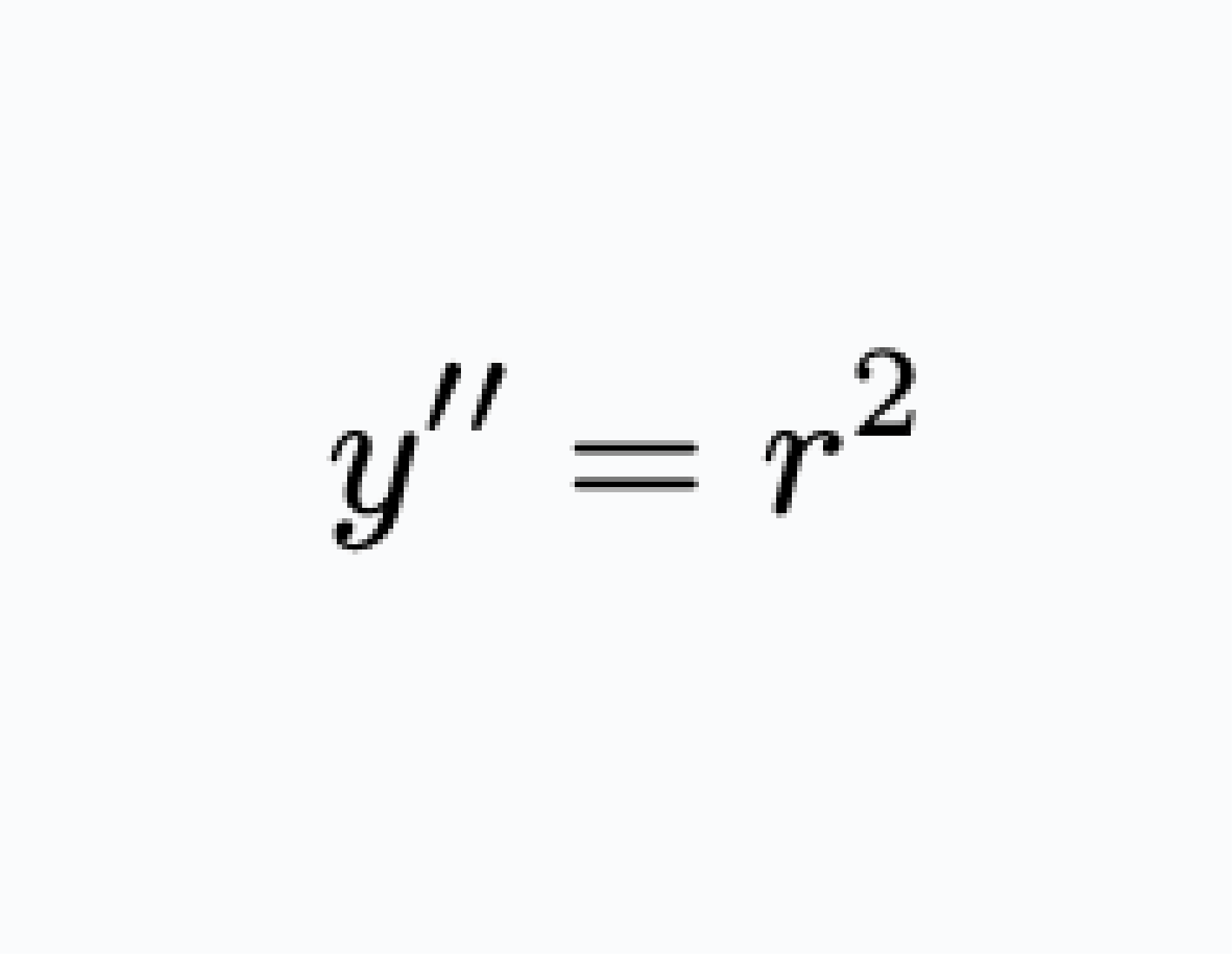Differential equations

A course in differential equations offers a comprehensive learning package contained in PDF documents covering a wide range of topics related to this area of mathematics. The materials provide key information on split variable equations, linear equations with constant coefficients and Bernoulli equations. To use the codes provided, it is necessary to download the dynpy library available in the button below. The selected code should then be pasted into the Jupyter Notebook project.


Dynpy Library

Download a PDF of the solved task

Display code

1. Equations with split variables

Equation with trigonometric functions

An example demonstrating the methodology for solving differential equations with separated variables using a trigonometric function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff(x)*sin(x)-y*cos(x),0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #w celu wywołania współczynników zmiennych rozdzielonych (odpowiednio x,y)
                                    odesys._function_separation()

                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()

                                    #aby uzyskać rozwiązanie
                                    odesys._ode_solution()

                                    #aby wygenerować raport z rozwiązaniem
                                    odesys.report

Equation with quadratic function

An example demonstrating the methodology for solving differential equations with separated variables using a quadratic function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(2*x**2*y.diff(x)+y,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #w celu wywołania współczynników rozdzielonych zmiennych (odpowiednio x,y)
                                    odesys._function_separation()

                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiazaniem
                                    odesys.report

Equation with a linear function

An example demonstrating the methodology for solving differential equations with separated variables using a linear function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*
                                    
                                    x=Symbol('x')
                                    y=Function('y')(x)
                                    
                                    #tu wprowadzić równanie:
                                    eq=Eq(5*x*y.diff(x)+y,0)
                                    
                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=HomogeneousSeparableODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)
                                    
                                    #w celu wywołania współczynników rozdzielonych zmiennych (odpowiednio x,y)
                                    odesys._function_separation()
                                    
                                    #w celu wywołania poszczególnych wyrażeń oraz całek zmiennych rozdzielonych
                                    odesys._function_integration()
                                    
                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()
                                    
                                    #aby wygenerowac raport z rozwiazaniem
                                    odesys.report

2. Linear equations

Equation with a linear function

An example demonstrating the methodology for solving linear differential equations with constant coefficients using a linear function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(-6+y.diff()-8*x+2*y,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

Equation with trigonometric functions

An example demonstrating the methodology for solving linear differential equations with constant coefficients using a trigonometric function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff()+y*cos(x)-sin,0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

Equation with an exponential function

An example demonstrating the methodology for solving linear differential equations with constant coefficients using an exponential function.

PDF

 
                                  
                                    from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                    from sympy import*

                                    x=Symbol('x')
                                    y=Function('y')(x)

                                    #tu wprowadzić równanie:
                                    eq=Eq(y.diff(x)-exp(2*x)-y*exp(x),0)

                                    # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                    odesys=LinearWithConstCoeffODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                    #aby wyświetlić równanie z uzmiennioną stałą
                                    odesys._variation_of_constant()

                                    #aby uzyskac rozwiazanie
                                    odesys._ode_solution()

                                    #aby wygenerowac raport z rozwiązaniem
                                    odesys.report

3. Bernoulli equations

Equation with quadratic functions

An example demonstrating the methodology for solving Bernoulli-type differential equations using a quadratic function.

PDF

 
                              

                                from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                from sympy import*

                                x=Symbol('x')
                                y=Function('y')(x)

                                #tu wprowadzić równanie:
                                eq=Eq(y+x*y.diff(x)+x*y**2,0)

                                # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                odesys=BernoulliODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)

                                #w celu wywołania podstawień typowych dla rownan bernoulliego
                                odesys._bernoulli_substitution()

                                #w celu wywołania najwyższej potegi naszego rownania uzywamy metody:
                                odesys.get_nonlinear_power()

                                #aby uzyskac rozwiazanie
                                odesys._ode_solution()

                                #aby wygenerowac raport z rozwiazaniem
                                odesys.report

Equation with trigonometric function

An example demonstrating the methodology for solving Bernoulli-type differential equations using a trigonometric function.

PDF

 
                              

                                from dynpy.solvers.linear import ODESystem, SeparableODE, LinearWithConstCoeffODE, HomogeneousSeparableODE, BernoulliODE
                                from sympy import*
                                
                                x=Symbol('x')
                                y=Function('y')(x)
                                
                                #tu wprowadzić równanie:
                                eq=Eq(y+x*y.diff(x)+x*y**2,0)
                                
                                # w poniższej linii równanie zostaje wprowadzone w klasę zbudowaną pod równania jednorodne o zmiennych rozdzielonych
                                odesys=BernoulliODE(eq.lhs - eq.rhs,Matrix([y]),ivar=x ,ode_order=1)
                                
                                #w celu wywołania podstawień typowych dla rownan bernoulliego
                                odesys._bernoulli_substitution()
                                
                                #w celu wywołania najwyższej potegi naszego rownania uzywamy metody:
                                odesys.get_nonlinear_power()
                                
                                #aby uzyskac rozwiazanie
                                odesys._ode_solution()
                                
                                #aby wygenerowac raport z rozwiazaniem
                                odesys.report

4. Second order equations

First example with a homogenous equation

A basic example showcasing the methodology for solving second order differential equations on an examplary homogenous equation with constant coefficients.

PDF

 
                              

                                from dynpy.utilities.components.ode.pl import HomoPredictionIntroComponent, EquationDefinitionComponent, MainPredictionComponent, RootsAnalysisComponent
                                from dynpy.solvers.linear import ODESystem, HomoODE2ndOrderEN
                                from sympy import*

                                x=Symbol('x')
                                y=Function('y')(x)

                                #here input the equation:
                                odes=y.diff(x,2)-1/2*y.diff(x)+10*y

                                #here the equation is inputted into the python class dedicated to solving homogeneous differential equation of 2nd order
                                odesys=HomoODE2ndOrderEN(odes,dvars=y,ivar=x)

                                #to generate a report with step by step solution
                                odesys.report;

Second example with a homogenous equation

A basic example showcasing the methodology for solving second order differential equations on an examplary homogenous equation with constant coefficients.

PDF

 
                              

                                from dynpy.utilities.components.ode.pl import HomoPredictionIntroComponent, EquationDefinitionComponent, MainPredictionComponent, RootsAnalysisComponent
                                from dynpy.solvers.linear import ODESystem, HomoODE2ndOrderEN
                                from sympy import*

                                x=Symbol('x')
                                y=Function('y')(x)

                                #here input the equation:
                                odes=y.diff(x,2)-7*y.diff(x)+10*y

                                #here the equation is inputted into the python class dedicated to solving homogeneous differential equation of 2nd order
                                odesys=HomoODE2ndOrderEN(odes,dvars=y,ivar=x)

                                #to generate a report with step by step solution
                                odesys.report;