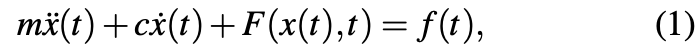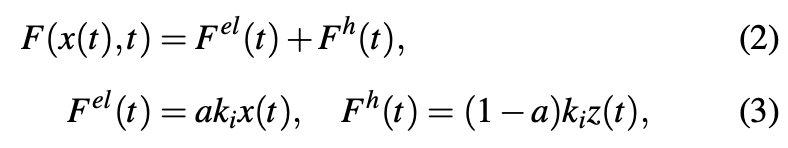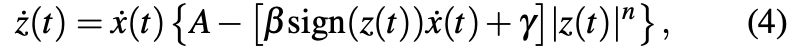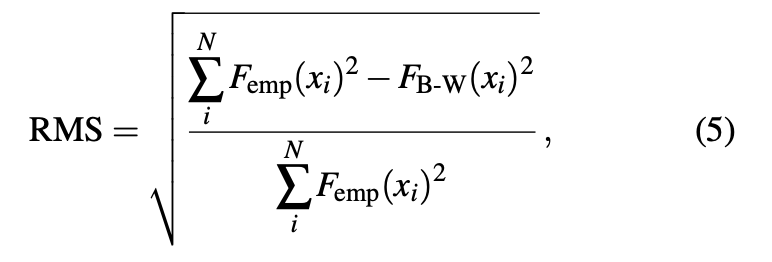Abstract
This paper concerns the problem of empirical investigation and mathematical modelling of a novel controllable damper using Vacuum
Packed Particles. Vacuum Packed Particles tend to be placed among the group of so-called ‘smart structures’. The macroscopic mechanical
features of such structures can be controlled by the partial vacuum parameter. The authors consider an application of Bouc-Wen model in order
to represent the dynamic behaviour of the investigated device. The verification of the model response with experimental data is discussed.
The Bouc-Wen model parameters identification is described.
1. Introduction
Mechanical vibration is a common phenomenon occurring in many branches of engineering. Depending on needs, they are
either a purposely generated factor necessary to implement specific technological processes or an undesirable phenomenon
accompanying the operations of machines and their components. In order to reduce and control the process of vibrations,
dampers are commonly used in a wide range of engineering
fields.
One might distinguish general types of dampers. The interesting examples are those based on variable and controllable
physical properties of magnetorheological (MR) or electrorheological (ER) fluids [1]. They belong to the group of smart materials that have been an object of an industrial and scientific interest over the years. Working principle of MR damper is based
on a reaction of a mixture of oil and magnetic particles on an
external magnetic field. This phenomenon ensures an external
factor, which allows to control damper characteristics. It provides an interesting mechanism for the damper dynamics control [2–4] that allows us to introduce a significant adjustment of
the damper response [5, 6].
Another group of controllable dampers are electrorheological
fluid (ERF) dampers. The idea of this kind of devices is based
on the interaction between ferromagnetic particles and an external electric field. Interesting control strategies can be applied
with a utilization of ERF dampers [7]. The evidence suggest
that it is possible to use it in order to control engineering structures dynamics.
Contrary to the aforementioned MR and ER fluids, a new
type of smart material referred as Vacuum Packed Particles
(VPP) is not yet fully recognized [8,9]. The mechanical characteristics of VPPs such as shape, stiffness or damping are easy to
change and control. The term “granular material under the vacuum conditions” refers to a structure made of plastomer grains.
The loose grains are enclosed in a hermetic and flexible envelope. The air is being pumped out of the hermetic container generating an underpressure causing the controllable and reversible
changes in the mechanical properties of the system [10]. VPP
allow to introduce innovative vibrations attenuation and control
strategies thanks to their lower cost in comparison with usually utilised MR or ER materials. Many potential applications
of VPP can be found as it might be applied to the elements of
any shape to control their vibrations.
There are some theoretical and empirical considerations
about the static response of the granular specimen on external
load [11, 12]. Literature offers many examples, where VPP are
used as a flexible element available to fit its outline to the specific shape of a cooperating element [13]. It is a base for numerous types of “smart” grippers, which enable us to grab and move
elements with non-regular surface [14]. Moreover, this “material” can be utilized as an active element of adjustable dampers,
which are competitive to MR or ERF dampers [9, 15, 16]. The
biggest advantage of those structures is a relatively low manufacturing and operating cost. Concepts of tuneable elements
utilising VPPs are described in some works and show efficient
control strategies [11]. Regarding shaping and control of the
dynamics with smart materials, the authors of [17] studied on a
new type of smart structure, which is a so-called sponge particle
structure (SPS). The authors proposed a method for controlling
the dynamics of a slender beam filled with SPS by shaping its
frequency structure by redistribution of the investigated system
mass.
Many practical applications of VPP-based devices might be
incorporated into medicine. A direct example of the practical
utilisation of the granular damper features is a vacuum mattress
– a medical device used for immobilization of patients, especially in the case of vertebra, pelvis or limb trauma [18].
2. Objectives
The aim of this paper is to preliminarily investigate a prototype
of a symmetrical controllable granular damper in the numerical and empirical manner. Analysis of the concept, design of
prototype and preliminary experiments are the main goals of
this study. Moreover, the assumed mathematical model is proposed in order to enable further theoretical analysis and identification/validation.
The biggest disadvantage of the existing VPP dampers designs is non-symmetrical stiffness and viscous characteristics.
Such a phenomenon is caused by observed differences in a loading axial forces values related to compression and elongation of
the cylinder samples made of VPP [19]. Moreover, during the
elongation process of the structure, the envelope plays a significant role and makes the entire structure stiffer [20]. In the case
of compression, stiffness of the hermetic sleeve is several times
lower (due to surface buckling) and does not affect the system
under consideration. It results in a completely different resistant
force for negative and positive values of damper clamps relative
displacement.
It this paper an innovative construction of the VPP damper
with symmetrical damping characteristics is proposed and discussed in details. The novel system with doubled VPP component on the both sides of the device is proposed. Simultaneously, one elastic element is compressed when the other is tensioned. This implies the resultant force to be always the same
and having a form of a sum of tensioning and compressing components.
3. Damper prototype
3.1 Prototype description
The proposed concept of a damper with symmetrical characteristics was configured as a set of granular structures. The prototype is composed of: several granular elastic elements, three
plates supporting the connectors, pushing rod and thin columns
which ensure the distance between outer plates and allow a
proper motion of the middle plate. The last part is a slider connected with a side disk by the granular connectors. An inner
plate can move to the left or right side along the columns. free
connectors limit the slider motion. The described solution is
presented in Fig. 1.
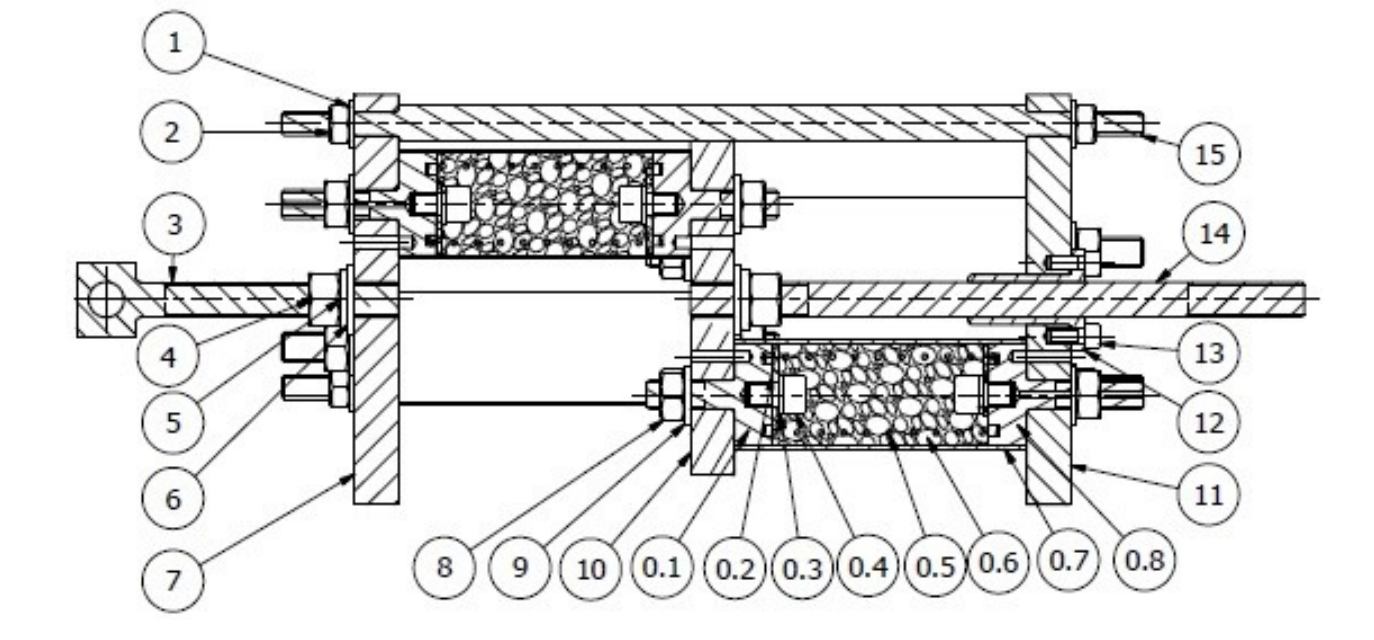
Fig. 1. Design of the granular damper prototype – cross-section view
(1 – guiding rod; 2 – fixing nut; 3 – handle; 4 – nut; 5,6 – pads; 7 –
lower disc; 8 – fastening nut; 9 – cylinder nut; 10 – middle movable
plate; 11 – upper plate; 13 – slider fastening nut; 14 – guiding rod; 15
– fixing nut; 0.1–0.8 – elements of the inner VPP cylinder)
The proposed prototype has a symmetric characteristics. It is
assured by an appropriate connection between the side plates.
When one side is compressed then the elements on the other
will be tensioned. The damper operates in the negative and positive direction at the same time as the two opposite sides are
actuated simultaneously. This simple solution ensures the desired behaviour eliminating the response discrepancy in tension
and compression.
3.2. Possible applications
The former experimental results indicate the feasibility of applying VPP to control vibrations of mechanical elements. In
order to damp oscillating motions of mechanical components,
the granular damper prototype needs to be implemented so that
the vibrating part is enclosed in a flexible envelope filled with
granulated polymers or any other non-polymer granules, where
the applied underpressure increases or decreases the compression of the granules, causing the system to become more or
less rigid. This, in turn, increases or decreases the energy dissipation, which provides the damping control mechanism of the
system vibrations. It can be stated that the properties mentioned
provide the possibility to design efficient devices with an application to machine elements such as beams, rods, plates, robotic
arms etc. in order to attenuate their vibrations.
When the air is pumped out of the sleeve, the generated underpressure causes the grains to compact so that the structure
becomes more rigid and its internal damping, caused by the
friction among the grains, increases. In this manner, one can
easily and effectively control the shape, stiffness, and damping
characteristics of the mechanical element.
Previous consideration indicates that mechanical properties
of a granular damper are strictly connected with working principle of this device [9]. It introduces some utilization barriers for
dampers based on VPP. Generally, it can be stated that granular
dampers are better for slowly vibrating designs due to high friction force and possible heat production. Moreover, asymmetric
hysteresis loop is a considerable limitation, which makes the
application difficult [15]. However, concept presented in this
work allows to omit those operational issues and enable the solution to satisfy requirements of engineering designs, especially
in civil engineering structures.
Operational time of VPP-based designs is one of the most
crucial problems. It is strictly connected with a wear and high
friction inside the VPP structure [21]. Therefore, a wear of the
damper may be neglected in short-term applications, damping
buildings or bridges during an earthquake what brings some
potential application also in civil engineering. Shape Memory Alloys often need to be replaced soon after the earthquake
episode. However, they increase the safety level in case of an
emergency [22]. Applying harder grains would address this
problem but this in turn significantly changes the damper properties. Depending on working conditions filling of the VPP
damper should be selected appropriately
4. Experiments
The purpose of the experimental research described in this article was to investigate the influence of changes in underpressure value on the mechanical properties of the grain material by assessing the density of energy dissipated during one cycle.
Tests of the symmetrical granular damper prototype having the dimensions of the global cylindrical shape including
250 mm diameter and 400 mm length were carried out for a
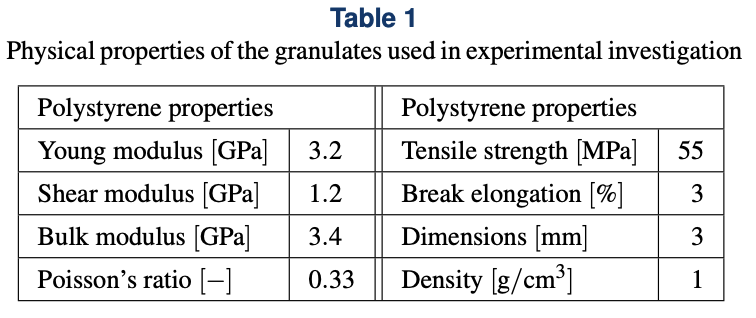
specific type of granular material. The polystyrene (PS) grains
serve as a filling of the elastic connectors of damper prototype.
The single grain has mechanical properties as specified in Table 1.
The experimental studies were carried out on the SHIMADZU EZ-LX testing machine equipped with a force load
cell of a maximum 5000 N depicted in Fig. 2. The prototype
of the symmetrical damper was mounted in clamps – one being
fixed and the other movable, through which sine kinematic excitation was applied. The tests were carried out for underpressure
value being in range of 0 MPa to 0.09 MPa. During the experiments, specified displacement and velocity of the exciter were
applied, while a force and the actual displacement and velocity
of the clamp were measured in time. Results in the form of a
hysteresis loops for the granular material type tested at various
undepressures are presented and discussed further in the article.
Fig. 2. Test stand
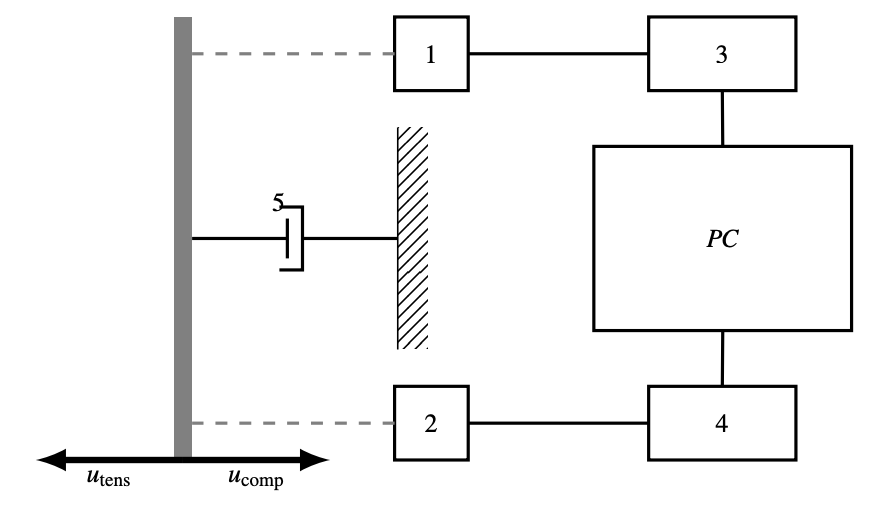
The measuring system utilised during the tests is presented
on the scheme in Fig. 3. The measuring system is composed
of two simultaneously operating sensors depicted as 1 and 2 in Fig. 3. First device measures the displacement of the specimen moving clamp. Force measurement are performed using the piezoelectric force sensor being able to register the force in a range of 10 N to 5000 N. Both detectors were plugged to DAQ devices presented as 3 and 4. These are analog-digital converters with sampling frequency of 1024 Hz connected to a computer (PC) for data acquisition.
Fig. 3. Scheme of the measuring system used. 1 – displacement
sensor, 2 – force sensor, 3, 4 – DAQ devices, 5 – investigated
damper, u_tens – facing of tensioning of a specimen, u_comp – facing
of compressing of a specimen
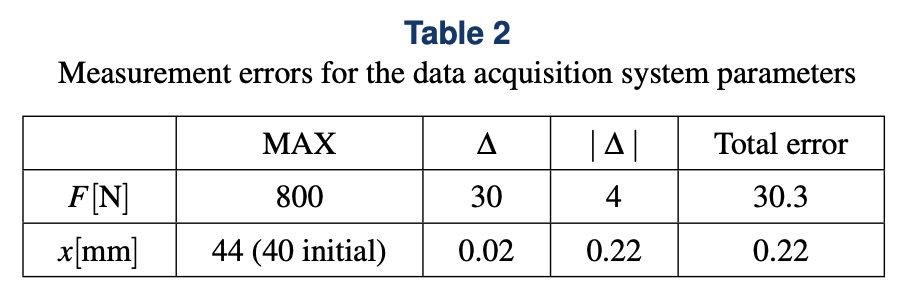
The experimental results are provided in Figs. 5–6. For the identification purposes, only one loop for arbitrary values of the underpressure was analysed. The reference cycle was obtained by averaging of five periods of the recorded signals. During this process, a standard deviation was estimated for the results ob- tained. All of the errors are presented in Table 2, where MAX is a maximum value of the analysed parameter, ∆ stands for de- viation of the analysed parameter, | ∆ | represents an absolute error and the last column is a total error of the tests performed.
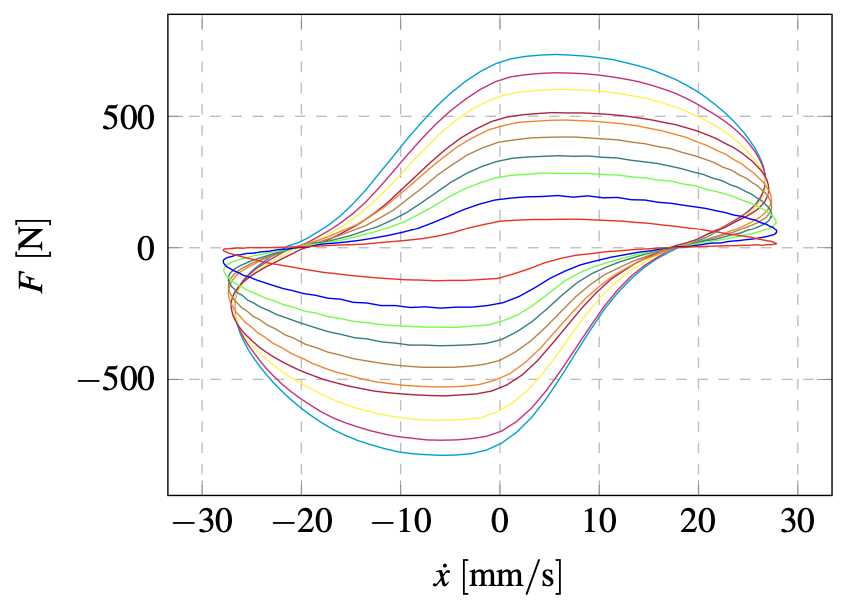
The results are presented in a form of force diagrams as a function of displacement F(x) and velocity F(x ̇), grouped so that the effect of the applied underpressure can be observed in both types of hysteretic characteristics F(x), F(x ̇) of the analysed symmetrical granular damper for various combina- tions of granules.
In experimental studies the authors used the polystyrene gran- ules shown in Fig. 4. Polystyrene is a granulate characterised with various visco-elastic properties which reflects in a much higher Young modulus, compressive strength and coefficient of friction comparing to other types of materials. In addition, one might observe that the granules have uniform dimensions and shapes, which results in a significant influence of the clusters occurring inside the sealed housing of the VPP damper.
Fig. 4. VPP damper filled with polystyrene
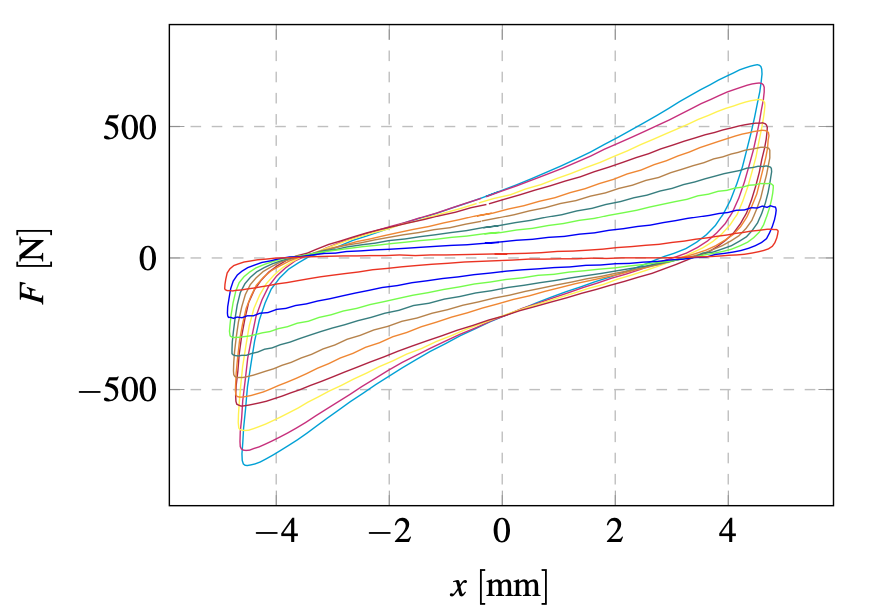
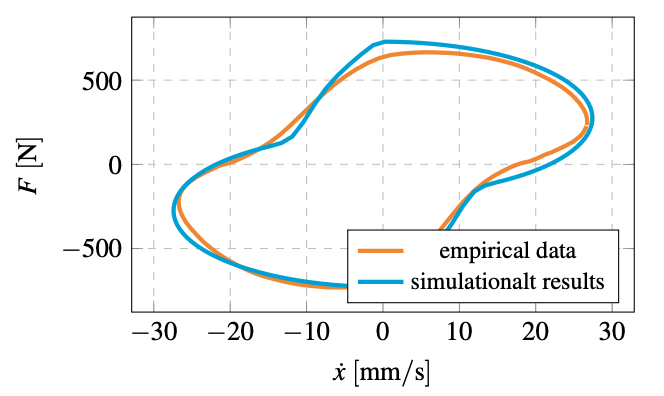
Fig. 5. Hysteresis loops registered for a variety of underpressure values for PS type of material (displacements)
Fig. 6. Hysteresis loops registered for a variety of underpressure values for PS type of material (velocities)
Figures 5 and 6 depict the experimental results. The tests were carried out to cover various values of underpressure. Based on data presented in Figs. 5 and 6 it can be stated that polystyrene granules allowed us to obtain quite high values of damping forces. However, the utilisation of this material might cause some potential operational problems as some powdered polystyrene material was found inside the damper after many compression cycles. This is a result of crushing the polystyrene granule which in further exploitation may lead to a reduction in the value of damping force as a function of the load cycles number carried out. In Fig. 4 one might notice some accumulation of the granular material in the central part of the damper. This phenomenon causes not only a reduction of damping force but an occurrence of the so-called dead zone at the damper operational range being a result of empty spaces between the two damper bases besides the granular material. These two phenomena affect the damper dissipative capability unfavourably and cause problems with sealing and durability of the matrix.
5. Proposition of Bouc-Wen model utilization
Modelling of metamaterials as VPP is a complex mechanical and mathematical problem. It is necessary to deal with a structure, which is composed of a large number of particles that then need to be simplified to enable engineering calculations. The Finite Elements Analysis or Discrete Elements Method are then commonly utilized. It is an explanation why phenomenological models could be interesting and useful [23].
Non-linear Bouc-Wen model of a damper was proposed in this paper. It is a single degree of freedom system with a lin- ear damping coefficient and non-linear elastic force [24]. The model under consideration is characterized by two main ele- ments: restoring action and hysteresis loop. It models elastic and hysteretic component by two different factors of the restor- ing force, which are fixed for the assumed system parameters. In this work, an extra dependency between VPP parameters was introduced which makes the proposed model sensitive to under pressure and grains physical parameters.
The mathematical model of the damper under consideration is as follows:
where: t – time, x(t) – displacement, m – oscillating mass, c – damping coefficient, F(x(t),t) – nonlinear elastic force, f(t) – resultant external force.
According to Bouc-Wen model, a decomposition of the restoring force F(t) can be done. Two parts components are distinguished, an elastic F_el(t) and a hysteretic F_h(t) force described as per the following formulas:
where: z(t) – non-observable hysteretic parameter, a – ratio of post-yield k_f to pre-yield k_i stiffness, k_i – ratio of the yield force to the yield displacement.
The hysteretic displacement z(t) is compliant with the following non-linear differential equation having a zero initial condition (z(0) = 0):
where: A, β , γ , n – dimensionless quantities controlling a behaviour of the considered model.
It was assumed that the influence of pressure and grains ar- rangement on the system dynamics can be described by an elas- tic component F_el(t) = F (x(t),t) only. The numerical simula- tions can be performed based on the proposed model. Prelimi- nary analysis shown that the model is sensitive to underpressure and operation time parameters [20]. Moreover, the proposed methodology of modelling can be efficient as it was presented in different studies [25]. Because of relative simplicity of the proposed model, it is proved that it can be successfully applied for a numerical and empirical data comparison. As a result of this process, the system equivalent parameters can be identified.
6. Numerical verification
The dynamic model of the granular damper prototype consid- ered within the article is determined by a second order ordinary differential equation (1). The transformation of the formula to the first order form enables its implementation to the numerical solver utilising some integrating method. The results of the in- tegration provide a basic information about the system dynamic behaviour. The ordinary differential equation was solved using the lsoda from the FORTRAN library odepack.
Based on that, numerical simulations of the investigated model prototype were carried out. The results of the numerical research are provided and discussed further within this section.
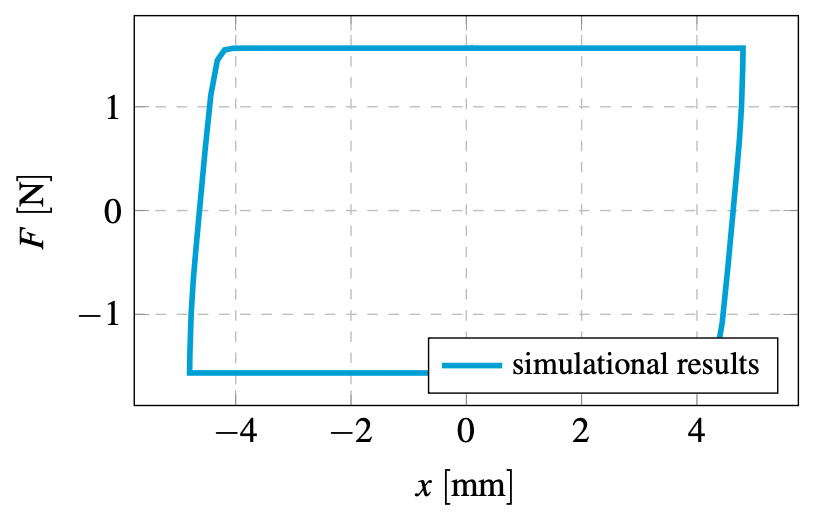
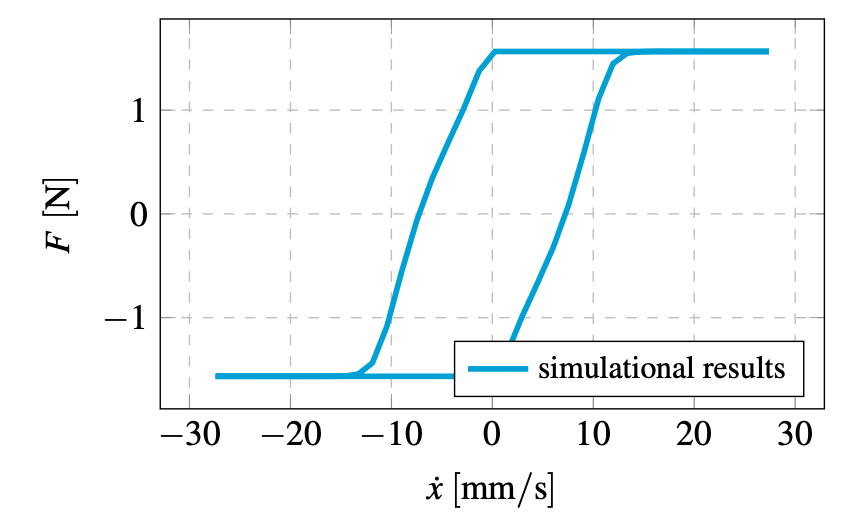
Fig. 7. Hysteresis loop for a B-W model parameters values a = 0.35, A = 6, β = 3.5, γ = −2.5, n = 4
Fig. 8. Hysteresis loop for a B-W model parameters values a = 0.35, A = 6, β = 3.5, γ = −2.5, n = 4
Results of the simulations carried out are depicted in Figs. 7 and 8. It is evident that a non-linear part of Bouc-Wen model enables the non-elastic properties of the considered material. From the modelling point of view, the proposed approach is especially useful for high values of n and β parameters - ob- tained results are close to behaviour of materials with a constant yield limit (bilinear characteristic). In order to estimate applied model parameters the following methodology further described in this subsection was used. For empirical results stiffness of the entire system was assumed. Based on that parameter, series of simulations were carried out with displacements and veloci- ties based on the experimental data. For the computed values, a relative RMS (Root Mean Square) error was calculated with a utilisation of formula (5).
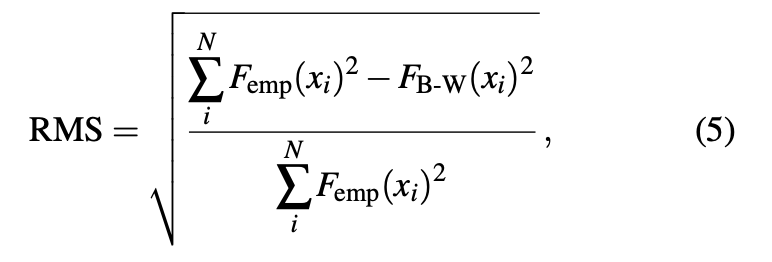
where: x_i – damper linear deformation for i step, N – number of probes, F_emp(x) – force value obtained during experiment, F_B-W (x) – computational force value.
The best results are presented in Figs. 9–16.
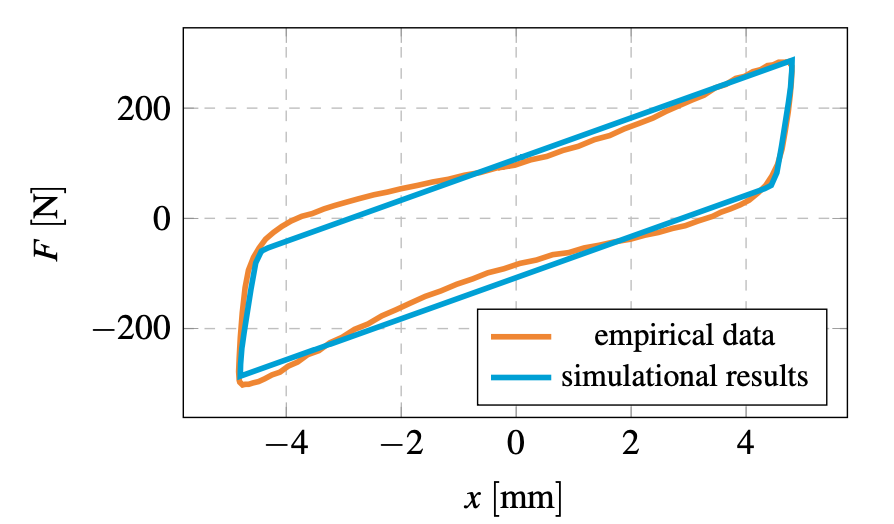
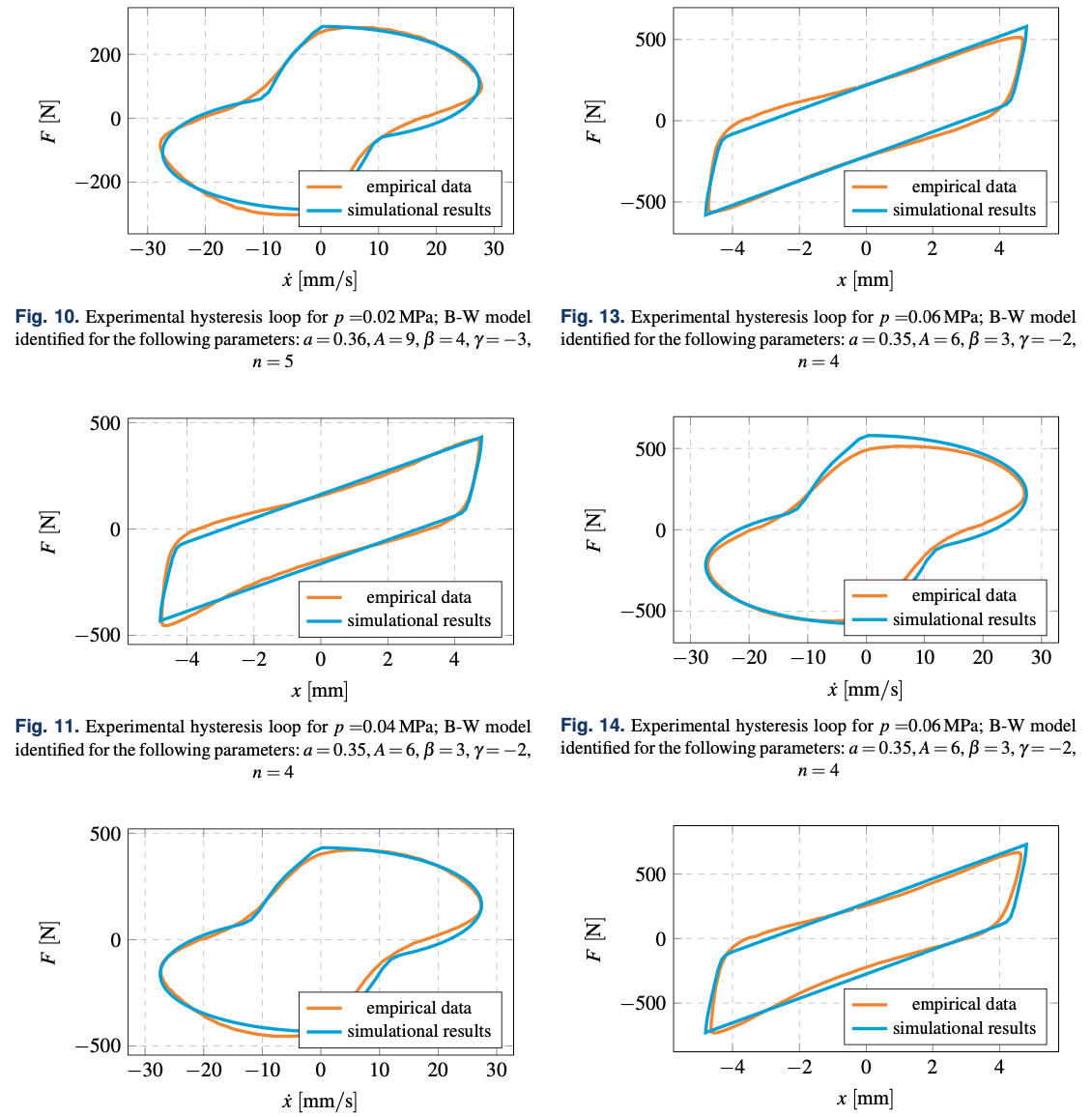
The conducted simulations outcome depicted in Figs. 9 and 10 show that for the assumed parameters of Bouc-Wen model, the obtained results are close to the empirical data. Some dis- crepancies are connected with the additional non-linear or dy- namic effects, which cannot be taken into account in the pro- posed approach. Still, the computed values model the proto- type in an acceptable way. The total RMS error was smaller than 0.01.
Fig. 9. Experimental hysteresis loop for p =0.02 MPa; B-W model identified for the following parameters: a = 0.36, A = 9, β = 4, γ = −3, n=5
Results presented in Figs. 11 and 12 correspond to the ef- fects of the previous simulations. Some discrepancies from the experiment are still visible but generally acceptable as the total RMS error was smaller than 0.006. It is evident that for the sub- sequent underpressure, the corresponding force extreme values are higher and that the proposed method model its behaviour accurately despite slight divergence.
The results of simulations for underpressure equals p = 0.06MPa (Figs. 13 and 14) indicate subsequent increasing of the force value. For this case the total RMS error was smaller than 0.0085. Numerous simulations were performed in order to achieve the best system parameters.
For the last case, the results of identification are presented in Figs. 15 and 16. The obtained values are similar to the previous simulations and reflect the prototype dynamic behaviour. For this case the total RMS error was smaller than 0.01.
In Figs. 17–20 the variations of the identified Bouc-Wen model parameters in the partial vacuum function are depicted. It should be stated that at the recent stage of the VPP damper research it is hard to define universal trends related to the model coefficients characteristics. Although basing on data presented in Figs. 17 and 20, A and n parameters values seem to stabilize for higher values of underpressure while similar dependencies
Fig. 16. Experimental hysteresis loop for p =0.08 MPa; B-W model identified for the following parameters: a = 0.34, A = 6, β = 2, γ = −1, n=4
for a and β parameters are not observed. To establish universal dependencies for the B-W model coefficients in the underpres- sure function, more complex experiments should be carried out. The parameters sets were determined by a systematic search al- gorithm and for each of the tested underpressures, some speci- fied RMS threshold value was set. As can be seen in Figs. 17, 18, 19 and 20, the range of values of each parameter appears very narrow or even becomes constant. The presented values represent the smallest RMS error that could have been achieved for each of the underpressure considered separately. Unfortu- nately, other sets of parameters produced, significantly worse mapping of the experimental hysteresis loops, and thus the error value exceeding the established RMS threshold for numerical simulations. For the future research the authors are going to im- plement more sophisticated identification procedure, based on heuristic algorithms (as Evolutionary Algorithms or Simulated Annealing). Modifying the initial form of Bouc-Wen model by introducing into it the non-linear functions of the underpres- sure will enable the engineers and researchers to carry out fast and reliable numerical simulations for novel controllable linear dampers.
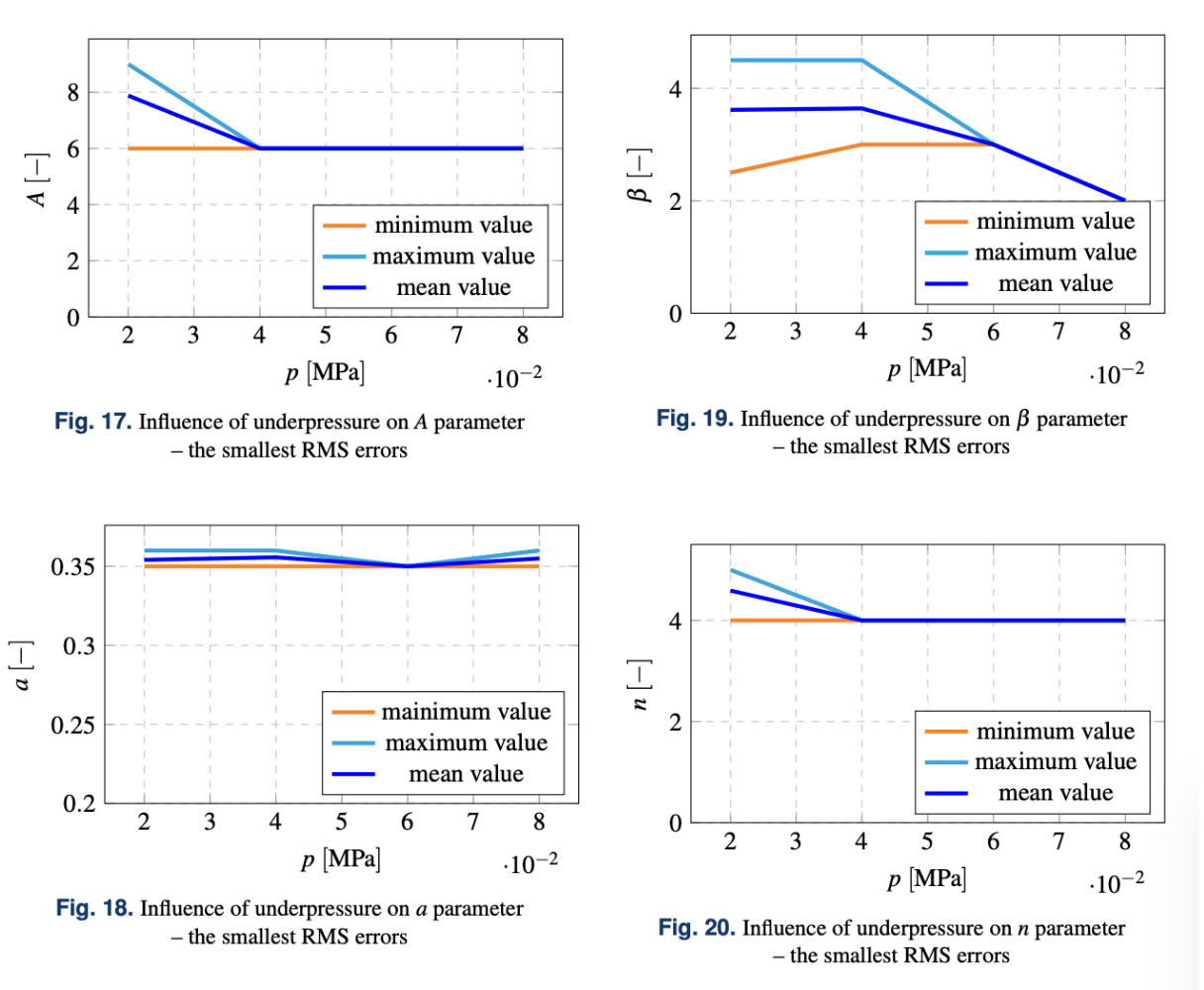
The simulations carried out allow to state the correctness of the proposed methodology. Bouc-Wen model which was uti- lized for the simulational purposes returns corresponding values as empirical data. The appropriate model parameters ensure the convergence of the numerical solution. Unfortunately, they de- pend on the control parameter in the form of the underpressure inside the structure. However, the minimal and maximal value equivalent parameters are similar. It allows to estimate optimal value of the model parameters as the mean value as presented in Figs. 18–20.
7. Summary
The control of vibrations with an absorber made of granular material has been modelled, numerically simulated and exper- imentally verified. Pumping air out of or into the envelope increases or decreases the compression of the granules, causing the system to become more or less deformable. This, in turn, increases or decreases the dissipation energy, which provides the damping control mechanism of the system vibrations. The changes to the dissipative characteristics of the damper caused by the rearrangement and compacting of the granules were described by a Bouc-Wen model. A numerical algorithm for the problem was presented along with the simulations results with special attention to the changes in oscillations as the grain rearrangement progresses. Then, the executed predictions were compared to the experimental results and proven good conver- gence with a discrepancy measured by RMS within a generally acceptable range.
The main observations gained are presented below:
1. Underpressure allows us for significant, macroscopic changes in the mechanical properties of the examined structure.
2. An increase in underpressure value causes a significant increase in the damper stiffness and increases the damping properties.
3. A utilisation of hard granulates as polystyrene allows us to obtain higher forces, but leads to a number of negative effects mainly increased wear of the granular core by crushing, abrasion and aggregation.
4. Dissipative characteristics and hysteresis loop are non-linear.
5. According to theoretical assumptions, it is possible to obtain a symmetry of forces during tensioning and compressing the damper. This was proven in practice but some inaccuracies may be encountered: leaks, inaccurate assembling in the neutral position and uneven distribution of granular material in the individual VPP damper. Those should be managed at the engineering and procedural level.
6. Proposed novel concept is characterised by symmetrical mechanical features. This distinguishes the presented design from the existing solutions, which are exclusively of an asymmetrical character.
7. A Bouc-Wen model of the proposed design has almost constant parameters corresponding with the hysteresis loop. That makes the identification process much easier comparing to procedures presented in the referred papers. The authors checked the response of the model for the selected values of nonlinear parameters and observed that the convergence of simulations and empirical results is satisfactory.
It is concluded that a granular material damper may be an easy to implement and cost effective way to dampen vibrations in mechanical systems.
References
[1] C. Graczykowski and P. Pawłowski, “Exact physical model of magnetorheological damper,” Appl. Math. Modell., vol. 47, pp. 400–424, 2017, doi: 10.1016/j.apm.2017.02.035.
[2] M. Makowski and L. Knap, “Reduction of wheel force varia- tions with magnetorheological devices,” J. Vib. Control, vol. 20, no. 10, pp. 1552–1564, 2014, doi: 10.1177/107754631247 2916.
[3] P.Martynowicz,“Studyofvibrationcontrolusinglaboratorytest rig of wind turbine tower-nacelle system with mr damper based tuned vibration absorber,” Bull. Pol. Acad. Sci. Tech. Sci., vol. 64, no. 2, pp. 347–359, 2016, doi: 10.1515/bpasts-2016-0040.
[4] T. Butz and O. v. Stryk, “Modelling and simulation of electro- and magnetorheological fluid dampers,” ZAMM – J. Appl. Math. Mech., vol. 82, no. 1, pp. 3–20, 2002, doi: 10.1002/1521-4001 (200201)82:1 3::AID-ZAMM33.0.CO;2-O.
[5] J. Wang and G. Meng, “Magnetorheological fluid devices: Prin- ciples, characteristics and applications in mechanical engineer- ing,” Proc. Inst. Mech. Eng., Part L: J. Mater.: Des. Appl., vol. 215, no. 3, pp. 165–174, 2001, doi: 10.1243/146442001154 5012.
[6] G. Yang, B.F. Spencer Jr, H.-J. Jung, and J.D. Carlson, “Dy- namic modeling of large-scale magnetorheological damper sys- tems for civil engineering applications,” J. Eng. Mech., vol. 130, no. 9, pp. 1107–1114, 2004, doi: 10.1061/(ASCE)0733- 9399(2004)130:9(1107).
[7] C.A.Vivas-Lopez,D.Hernández-Alcantara,R.Morales-Menen- dez, R.A. Ramírez-Mendoza, and H. Ahuett-Garza, “Method for modeling electrorheological dampers using its dynamic charac- teristics,” Math. Probl. Eng., 2015, doi: 10.1155/2015/905731.
[8] M. Cates, J. Wittmer, J.-P. Bouchaud, and P. Claudin, “Jamming, force chains, and fragile matter,” Phys. Rev. Lett., vol. 81, no. 9, p. 1841, 1998, doi: 10.1103/PhysRevLett.81.1841.
[9] R. Zalewski and P. Chodkiewicz, “Semi-active linear vacuum packed particles damper,” J. Theor. Appl. Mech., vol. 54, no. 1, pp. 311–316, 2016, doi: 10.15632/jtam-pl.54.1.311.
[10] A. Jiang, T. Aste, P. Dasgupta, K. Althoefer, and T. Nana- yakkara, “Granular jamming with hydraulic control,” Am. Soc. Mech. Eng., vol. 55935, 2013, doi: 10.1115/DETC2013-12213.
[11] J.M. Bajkowski, B. Dyniewicz, and C.I. Bajer, “Semi-active damping strategy for beams system with pneumatically con- trolled granular structure,” Mech. Syst. Sig. Process., vol. 70-71, pp. 387–396, 2016, doi: 10.1016/j.ymssp.2015.09.026.
[12] R. Zalewski and T. Szmidt, “Application of special granular structures for semi-active damping of lateral beam vibrations,” Eng. Struct., vol. 65, pp. 13–20, 2014, doi: 10.1016/j.eng struct. 2014.01.035.
[13] A.J. Loeve, O.S. van de Ven, J.G. Vogel, P. Breedveld, and J. Dankelman, “Vacuum packed particles as flexible endoscope guides with controllable rigidity,” Granular Matter, vol. 12, no. 6, pp. 543–554, 2010, doi: 10.1007/s10035-010-0193-8.
[14] E.Brownetal.,“Universalroboticgripperbasedonthejamming of granular material,” PNAS, vol. 107, no. 44, pp. 18 809–18 814, 2010, doi: 10.1073/pnas.1003250107.
[15] R. Zalewski, P. Chodkiewicz, and M. Shillor, “Vibrations of a mass-spring system using a granular-material damper,” v, vol. 40, no. 17, pp. 8033–8047, 2016, doi: 10.1016/j.apm.2016. 03.053.
[16] D. Rodak and R. Zalewski, “Innovative controllable torsional damper based on vacuum packed particles,” Materials, vol. 13, no. 19, p. 4356, 2020, doi: 10.3390/ma13194356.
[17] M.Z ̇urawski,B.Chilin ́ski,andR.Zalewski,“Anovelmethodfor changing the dynamics of slender elements using sponge parti- cles structures,” Materials, vol. 13, no. 21, p. 4874, 2020, doi: 10.3390/ma13214874.
[18] M.D. Luscombe and J.L. Williams, “Comparison of a long spinal board and vacuum mattress for spinal immobilisation,” Emer- gency Med. J., vol. 20, no. 5, pp. 476–478, 2003, doi: 10.1136/ emj.20.5.476.
[19] P. Bartkowski and R. Zalewski, “A concept of smart multiaxial impact damper made of vacuum packed particles,” MATEC Web of Conferences, vol. 157, p. 05001, 2018, doi: 10.1051/matec- conf/201815705001.
[20] P. Bartkowski, R. Zalewski, and P. Chodkiewicz, “Parameter identification of bouc-wen model for vacuum packed particles based on genetic algorithm,” Arch. Civ. Mech. Eng., vol. 19, no. 2, pp. 322–333, 2019, doi: 10.1016/j.acme.2018.11.002.
[21] R. Zalewski and M. Pyrz, “Experimental study and modeling of polymer granular structures submitted to internal underpres- sure,” Mech. Mater., vol. 57, pp. 75–85, 2013, doi: 10.1016/ j.mechmat.2012.11.002.
[22] A. Zbiciak and K. Wasilewski, “Constitutive modelling and nu- merical implementation of sma material with internal loops,” Arch. Civ. Eng., vol. 64, no. 4/I, 2018, doi: 10.2478/ace-2018- 0053.
[23] M. Sánchez, G. Rosenthal, and L.A. Pugnaloni, “Universal re- sponse of optimal granular damping devices,” J. Sound Vib., vol. 331, no. 20, pp. 4389–4394, 2012, doi: 10.1016/j.jsv.2012. 05.001.
[24] R. Bouc, “Forced vibration of mechanical systems with hystere- sis,” Proceedings of Fourth Conference on Non-Linear Oscilla- tion, Prague, 5-9 September 1967.
[25] M. Ismail, F. Ikhouane, and J. Rodellar, “The hysteresis bouc-wen model, a survey,” Arch. Comput. Methods Eng., vol. 16, no. 2, pp. 161–188, 2009, doi: 10.1007/s11831-009-90 31-8.